조셉슨 접합의 MQT, 열 활성화를 넘어선 퀀텀 현상의 발견: Devoret, Martinis, Clarke 논문이 증명한 양자 역학의 보편성
안녕하세요! 오늘은 제가 정말 감명 깊게 읽었던 논문, 바로 "Devoret, Martinis, Clarke Measurements of Macroscopic Quantum Tunneling out of the Zero-Voltage State of a Current-Biased Josephson Junction 전류 바이어스된 조셉슨 접합의 영전압 상태에서 거시적 양자 터널링의 측정"에 대한 학습 노트를 공유하려고 해요. 제목부터 엄청나게 전문적인 느낌이죠? 저도 처음엔 '이걸 내가 정확하게 이해할 수 있을까?' 싶었는데, 읽고 나니 왜 이 논문이 양자 컴퓨팅과 초전도 연구의 역사에서 중요한 이정표가 되었는지 알겠더라고요.
솔직히 말해서, 거시적 양자 터널링(Macroscopic Quantum Tunneling, MQT)이라는 개념 자체가 좀 신비롭잖아요. 미시 세계의 전유물이라 생각했던 양자 역학적 현상이, 눈으로 볼 수 있을 만큼 '거시적인' 크기인 조셉슨 접합(Josephson Junction) 회로에서 관측되었다는 사실! 이 실험이 성공적으로 진행되면서, 양자 역학이 단순히 원자나 분자 수준에만 국한된 게 아니라는 엄청난 증거를 제시했어요. 이 논문을 통해 저와 함께 그 짜릿한 발견의 현장 속으로 들어가 보실까요?
거시적 양자 터널링(MQT)의 개념과 측정의 핵심
우리가 이 논문을 제대로 이해하려면, 먼저 조셉슨 접합(Josephson Junction)이 무엇인지, 그리고 거시적 양자 터널링(MQT)이 정확히 어떤 의미인지 알아야 해요. 조셉슨 접합은 초전도체 두 개를 아주 얇은 절연층으로 분리해 놓은 구조물인데요, 이 접합은 기본적으로 두 가지 상태를 가질 수 있습니다. 바로 '전압이 없는 상태(Zero-Voltage State)'와 '전압이 있는 상태(Voltage State)'죠.
이 논문의 핵심은 조셉슨 접합이 전류 편향(Current-Biased)된 상태, 그러니까 일정한 전류가 흐르도록 설정된 상태에서 벌어지는 일이에요. 접합을 흐르는 위상차 δ 를 마치 입자의 위치 𝑥처럼 생각하고, 접합에 가해진 전류에 의한 에너지를 입자가 놓인 퍼텐셜 우물(Potential Well)로 간주할 수 있어요. 상상해 보세요. 퍼텐셜 우물은 비탈길 같은 건데, 입자는 일반적으로 이 비탈길을 넘어가지 못하고 우물 안에 머무르려고 하죠. 고전적인 물리학 관점에서는 입자가 우물(Zero-Voltage State)에서 벗어나기 위해선 반드시 충분한 에너지를 얻어 '장벽'을 넘어야 해요. 이 에너지를 넘지 못하면 입자는 영원히 우물 안에 갇혀 있어야 합니다.
하지만 양자 역학은 다른 이야기를 합니다. 바로 터널링 효과(Tunneling Effect)죠. 충분한 에너지가 없어도, 입자가 장벽을 뚫고 반대편으로 넘어갈 수 있다는 거예요! Devoret, Martinis, Clarke는 바로 이 양자 역학적 터널링이 미시적인 입자가 아니라 거시적인 변수인 조셉슨 접합의 위상차에서 발생할 수 있음을 실험적으로 증명하려고 했어요. 위상차 δ는 수많은 초전도 전자쌍(쿠퍼 쌍)의 거동을 나타내는 변수이기 때문에, 이것이 터널링을 한다는 것은 곧 거시적인 시스템이 양자 역학을 따른다는 의미가 됩니다. 이것이 바로 거시적 양자 터널링(MQT)의 정의예요. 정말 짜릿한 개념이지 않나요?
MQT는 거시적인 시스템 변수가 열 에너지 없이 양자 역학적 터널링을 통해 하나의 상태(제로 전압 상태)에서 다른 상태(전압 상태)로 전이하는 현상을 말합니다. 이 논문이 없었다면 양자 컴퓨터는 아마도 지금처럼 발전하기 어려웠을 거예요!
자, 그렇다면 이 MQT를 어떻게 측정했을까요? 저자들은 접합이 제로 전압 상태(퍼텐셜 우물)에 머무르는 시간을 측정하는 방식을 사용했어요. 만약 고전적인 열 활성화(Thermally Activated) 전이만 있다면, 낮은 온도(Low Temperature)에서는 전이가 거의 일어나지 않거나, 특정 온도 이하에서는 전이율이 급격히 줄어들어야 합니다. 하지만 양자 터널링이 우세하게 작동하는 영역에 도달하면, 온도가 아무리 낮아져도 전이율은 특정 값 이하로 떨어지지 않고 평평하게 유지되어야 하죠. 이것이 바로 MQT를 확인하는 결정적인 '지문'입니다.
Devoret, Martinis, Clarke는 이 '지문'을 찾기 위해 매우 정교한 실험 설계를 했어요. 그들은 조셉슨 접합을 매우 낮은 온도(수 mK, 밀리켈빈)에서 작동시켜 열 에너지의 영향을 최소화했습니다. 그리고 접합에 가해지는 전류 𝐼를 정밀하게 조절하면서 접합이 제로 전압 상태에서 벗어나 전압 상태로 넘어가는 '탈출 빈도(Escape Frequency)' 또는 '탈출 확률'을 측정했죠. 이 거시적 양자 터널링 측정은 노이즈를 극도로 줄이고, 외부 환경과 완벽하게 분리하는 것이 관건이었어요. 이분들이 얼마나 대단한 엔지니어링 능력을 보여줬는지, 논문을 읽는 내내 감탄이 나왔습니다. 이 실험의 성공은 양자 역학의 기본 원리가 거시 세계에서도 유효함을 입증한 것이자, 후속 연구를 위한 중요한 발판을 마련한 일이었어요. 단순히 측정을 했다는 사실을 넘어, 양자 현상을 제어하고 활용할 수 있는 가능성을 열어줬다는 점에서 거시적 양자 터널링 연구의 가치는 정말 높다고 생각해요.
실험 설계의 디테일과 측정 결과의 명확성
논문을 읽으면서 가장 인상 깊었던 부분은 저자들이 실험의 노이즈와 외부 환경 영향을 얼마나 철저하게 배제하려고 노력했는지에 대한 디테일이었어요. 거시적 양자 터널링을 관측하는 건, 마치 아주 조용한 새벽에 멀리서 들려오는 작은 속삭임을 들으려는 것과 같거든요. 조금이라도 잡음이 섞이면 진짜 양자 효과인지, 아니면 단순한 열 잡음(Thermal Noise) 때문인지 구별할 수가 없으니까요. 이분들은 특히 접합의 유효 질량(Effective Mass)과 저항을 조절하는 데 많은 공을 들였습니다.
그들이 사용한 조셉슨 접합은 알루미늄(Al)을 이용한 터널링 접합이었는데, 낮은 온도에서 초전도 상태를 유지하면서도, 양자 역학적 효과가 두드러지게 나타날 수 있도록 임계 전류 I0와 접합 커패시턴스 C값을 세밀하게 조정했어요. 조셉슨 접합은 기본적으로 'RCS 모델(Resistively and Capacitively Shunted Junction model)'로 설명되는데, 이 모델에서 접합의 유효 질량은 커패시턴스 C에 비례하고, 장벽의 높이는 임계 전류 𝐼0와 편향 전류 𝐼에 의해 결정됩니다. 거시적 양자 터널링이 일어나기 위한 조건, 즉 양자 영역(Quantum Regime)으로 진입하려면, 이 접합 커패시턴스가 충분히 커서 유효 질량이 무거워야 하고, 동시에 환경과의 결합(저항 성분)은 최소화되어야 합니다.
거시적 양자 터널링 측정에서는 외부 노이즈나 고주파 복사가 퍼텐셜 장벽을 흔들어 열 활성화 전이처럼 보이게 만들 수 있어요. 저자들은 이를 막기 위해 다양한 차폐 기법과 필터링 기술을 동원했습니다. 이 노력이 없었다면 MQT는 열 잡음에 묻혀버렸을 거예요!
측정 결과는 정말 명확했어요. 온도를 100 mK 이하로 낮추자, 접합의 탈출 빈도 𝛤가 더 이상 온도에 의존하지 않고 특정한 값(잔류 값)으로 수렴하는 것을 관측했습니다. 바로 이것이 거시적 양자 터널링의 확실한 증거인 거죠! 고전적인 열 활성화 이론 Γₜₕₑᵣₘₐₗ ∝ e⁻⁽ᵁ⧸⁽ᵏᴮ×ᵀ⁾⁾ 에 따르면, 온도가 0에 가까워질수록 (T → 0) 탈출 빈도는 기하급수적으로 줄어들어 0에 도달해야 하거든요. 그런데 실제 측정된 값은 0이 아니었습니다. 이 잔류 탈출 빈도는 양자 역학적 터널링 확률 (𝛤₍𝓺𝓾𝓪𝓷𝓽𝓾𝓶₎) 과 정확하게 일치하는 결과를 보여주었어요.
더 나아가, 저자들은 접합에 가해지는 편향 전류 (I) 의 크기를 변화시키면서 탈출 빈도가 어떻게 변하는지 측정했습니다. 이론적으로 거시적 양자 터널링 확률은 퍼텐셜 장벽의 높이와 두께에 매우 민감하게 의존하는데, 편향 전류가 커질수록 장벽이 낮아지고 얇아지기 때문에 터널링 확률은 기하급수적으로 증가해야 합니다. 실험 결과, 측정된 탈출 빈도는 WKB 근사(Wentzel–Kramers–Brillouin approximation)를 이용한 양자 역학적 예측과 거의 완벽하게 일치했어요! 이것이 이 논문의 또 하나의 결정적인 승리였습니다. 단순히 'MQT가 존재한다'를 넘어, MQT의 정량적인 행동까지 예측 모델과 부합한다는 것을 보여줬으니까요.
이러한 디테일한 접근 방식 덕분에, 이 논문은 단순히 초전도 물리학을 넘어 거시적인 시스템이 어떻게 양자 역학적 행동을 보일 수 있는지에 대한 가장 명확하고 깨끗한 증거를 제공했어요. 특히 양자 상태의 중첩과 결맞음(Coherence)을 이용하는 양자 컴퓨팅의 기반 이론을 다지는 데 결정적인 역할을 했다고 저는 확신해요. 이 논문이 없었다면, 아마도 오늘날 우리가 이야기하는 '양자 큐비트'의 구현은 훨씬 더 더뎠을 거라고 생각하면, 이분들의 선구적인 노력이 정말 대단하게 느껴집니다. 이렇게 정교하고 치밀한 실험을 해낼 수 있었다는 사실 자체가 놀랍지 않나요? 이 거시적 양자 터널링의 측정은 물리학의 오랜 질문에 대한 명쾌한 답을 제시해 준 것이나 다름없습니다.
양자 결맞음과 조셉슨 접합의 퍼텐셜 해석
이 논문의 심오한 매력은 단순히 거시적 양자 터널링을 관측했다는 사실을 넘어, 조셉슨 접합을 하나의 '양자 시스템'으로 해석할 수 있는 견고한 이론적 틀을 제시했다는 점이에요. 아까 제가 조셉슨 접합의 위상차 (δ) 를 입자의 위치처럼 본다고 말씀드렸죠? 이 비유가 바로 논문의 핵심 논리 중 하나인 조셉슨 접합의 퍼텐셜 우물 해석입니다.
조셉슨 접합의 에너지는 위상차 δ 에 따라 다음과 같은 퍼텐셜 에너지 함수로 표현됩니다: U(δ, I) = - EJ * cos(δ) - (h / 2e) * I * δ 여기서 EJ는 조셉슨 에너지이고, I는 외부에서 가해주는 편향 전류입니다. 저자들은 이 방정식을 통해 접합의 상태를 '입자가 놓인 퍼텐셜'로 시각화했어요. 편향 전류 I 가 없을 때는 주기적인 퍼텐셜이 되지만, 전류가 가해지면 퍼텐셜이 기울어지면서 국소적인 최소점(메타안정 상태)을 가지게 됩니다. 이 최소점이 바로 제로 전압 상태(Zero-Voltage State)에 해당하는 곳이에요.
양자 결맞음(Quantum Coherence)의 관점에서 볼 때, 이 메타안정 상태는 유한한 시간 동안만 안정적입니다. 입자(위상차)는 이 우물 안에 갇혀 있다가도, 고전적인 에너지 장벽을 넘을 수 없음에도 불구하고 터널링을 통해 다음 우물(전압 상태)로 넘어갈 수 있죠. 이 논문은 이 터널링 과정이 순수한 양자 역학적 과정임을 증명함으로써, 조셉슨 접합이 단순한 고전적인 비선형 회로가 아니라 양자 역학적 거동을 보이는 거시적 양자 시스템임을 확실히 입증했어요. 이게 왜 중요하냐고요? 조셉슨 접합을 양자 큐비트(Quantum Qubit)의 기초 단위로 활용할 수 있는 이론적 토대가 되었기 때문입니다.
퍼텐셜 장벽 계산
논문에서 제시된 것처럼, 장벽의 높이 (ΔU) 는 편향 전류 I와 임계 전류 I₀의 비율 i=I/I₀ 에 따라 결정됩니다. 편향 전류가 증가하면 장벽 높이는 낮아지고 폭은 좁아져 거시적 양자 터널링 확률이 기하급수적으로 증가하게 됩니다. 저자들은 이 ΔU 가 고전적 열 활성화와 양자 터널링 중 어떤 것이 지배적인지 결정하는 핵심 변수임을 명확히 보여주었습니다.
이론적으로 장벽 높이는 다음 식의 형태로 근사됩니다:
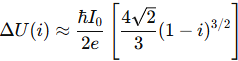
저자들의 통찰력은 단순히 측정을 넘어, 열 활성화 영역과 양자 터널링 영역 사이의 경계, 즉 교차 온도(Crossover Temperature, TCROSSOVER)를 명확하게 제시했다는 점입니다. 이 온도는 시스템의 특성(EJ, C, I)으로부터 이론적으로 계산될 수 있으며, 실제 실험에서 측정 온도가 이 TCROSSOVER 이하로 떨어질 때 비로소 온도에 무관한 MQT 현상이 관측된다는 사실을 입증했어요. 그들이 사용한 접합의 특성에 따라 이 TCROSSOVER는 수십 mK 수준이었는데, 이게 바로 저자들이 밀리켈빈(mK)까지 온도를 낮추는 극저온 기술을 사용해야 했던 이유이기도 합니다.
거시적 양자 터널링의 측정은 고전 물리학이 설명할 수 없는 영역을 실험적으로 포착했다는 점에서 물리학적으로 엄청난 의미를 가집니다. 특히, 양자 결맞음이 거시적인 변수 (δ) 에서도 일정 시간 동안 유지될 수 있음을 시사함으로써, 거시 세계와 미시 세계를 나누는 경계에 대한 우리의 이해를 넓혀줬다고 볼 수 있죠. 이 논문이 양자 정보 과학에 미친 영향을 생각해 보면, 단순한 실험 결과 보고서를 넘어선 하나의 철학적 발견이었다고 해도 과언이 아닐 것 같아요. 정말 깊이 있는 통찰이 담겨 있는 논문이라, 물리학에 관심 있는 분들이라면 꼭 한번 정독해 보시기를 추천합니다. 저도 이 논문을 읽으면서 양자 터널링에 대한 이해의 폭이 훨씬 넓어진 기분이었어요!
양자 컴퓨팅의 관점에서 본 MQT 연구의 역사적 의의
자, 이제 이 거시적 양자 터널링 연구가 왜 양자 컴퓨팅이라는 거대한 흐름에 그렇게나 중요한 영향을 미쳤는지 이야기해 볼 시간이에요. Devoret, Martinis, Clarke의 이 선구적인 논문은 단순히 물리학의 기초 이론을 확인한 것을 넘어, 실제로 양자 효과를 활용할 수 있는 기술적 가능성을 열어줬다는 점에서 역사적입니다.
양자 컴퓨터의 기본 단위인 큐비트(Qubit)는 '0'과 '1' 상태를 동시에 가질 수 있는 양자 중첩(Superposition) 상태를 유지해야 하잖아요? 초전도 큐비트, 특히 플럭스 큐비트(Flux Qubit)나 전하 큐비트(Charge Qubit)의 초기 모델들은 바로 이 조셉슨 접합을 기반으로 만들어졌어요. 이 접합을 양자 역학적으로 행동하게 만들려면, 접합의 거시적인 변수(위상차나 전하)가 고전적인 잡음이나 열 활성화로부터 격리된 채로 양자적 특성을 유지해야만 합니다.
이 논문이 거시적 양자 터널링을 명확히 증명하기 전까지는, 일부 학자들은 조셉슨 접합과 같은 거시적인 장치에서는 환경과의 결합 때문에 양자 효과가 빠르게 사라질 것(Decoherence)이라고 회의적으로 봤어요. 하지만 Devoret 팀의 실험은 매우 낮은 온도와 정교한 제어를 통해 MQT, 즉 거시적 양자 현상이 관측될 수 있음을 입증했죠. 이는 곧, 조셉슨 접합을 잘 다듬고 격리시키면 양자 중첩 상태를 유지하는 큐비트를 만들 수 있다는 희망의 청사진을 제시한 거나 마찬가지였어요!
특히, 이 논문에서 다룬 위상차의 퍼텐셜 우물 해석은 큐비트의 에너지 준위를 설계하는 데 결정적인 아이디어를 제공했어요. 제로 전압 상태(우물)에서 전압 상태(바깥)로 넘어가는 거시적 양자 터널링 과정은, 사실상 메타안정 상태 내에서 큐비트의 에너지 준위를 정의하고 제어하는 방식을 이해하는 데 필수적인 기초를 제공했습니다. 이 터널링 과정을 정밀하게 측정하고 제어하는 기술이 발전하면서, 초전도 큐비트의 스위칭 메커니즘을 이해하는 데 큰 도움이 되었죠.
거시적 양자 터널링은 초전도 큐비트에서 제로 상태와 전압 상태 사이의 양자 전이(Quantum Transition)를 이해하는 데 핵심적인 역할을 했어요. 이 현상의 발견이 없었다면, 양자 상태의 제어 가능성에 대한 확신이 부족했을 겁니다.
게다가, 논문에서 제시된 데이터의 정확성과 이론과의 완벽한 일치는 이 분야 연구자들에게 초전도 회로가 양자 역학의 법칙을 따르는 신뢰할 수 있는 플랫폼임을 강력하게 시사했어요. 그 이후로 수많은 연구팀이 이 논문을 기반으로 조셉슨 접합을 이용한 다양한 큐비트 아키텍처(Charge, Flux, Transmon 등)를 개발하기 시작했습니다. Transmon 큐비트처럼 더 안정적인 큐비트가 개발되었지만, 그 근본적인 양자 역학적 원리, 특히 퍼텐셜 우물에서의 에너지 준위와 전이 현상을 이해하는 데 있어 이 거시적 양자 터널링 논문의 역할은 절대 과소평가될 수 없어요.
제가 이 논문을 '전설적'이라고 부르는 이유가 바로 여기에 있습니다. 단순히 하나의 실험 결과가 아니라, 미래 기술인 양자 컴퓨팅의 기반을 다진 씨앗이 되었기 때문이죠. 이분들의 노력 덕분에 우리는 오늘날 구글, IBM 같은 거대 기술 기업들이 수십 개의 큐비트를 가진 양자 프로세서를 개발하는 시대를 맞이할 수 있게 되었어요. 거시적 양자 터널링의 측정은 물리학의 난제를 해결함과 동시에, 인류에게 새로운 계산 패러다임을 선사한 기념비적인 업적이었다고 생각합니다. 아, 진짜 이 논문은 시대를 앞서간 통찰력이 담겨 있어요.
고전적 활성화 이론과 양자 터널링 이론의 비교 분석
이 논문의 가장 강력한 논리적 무기는 바로 고전적 활성화 이론(Thermal Activation Theory)과 양자 터널링 이론(Quantum Tunneling Theory) 사이의 결정적인 비교 분석이었어요. 저자들은 이 두 이론이 예측하는 탈출 빈도 (𝛤) 의 온도 의존성을 명확히 구분하고, 실험 데이터를 통해 어느 이론이 현실을 더 잘 설명하는지 보여줬습니다. 이 과정이 정말 짜릿한 과학적 논리 전개였죠!
먼저, 고전적 활성화(Thermal Activation) 이론부터 살펴볼까요? 이 이론은 조셉슨 접합이 제로 전압 상태(퍼텐셜 우물)에서 벗어나 전압 상태로 전이하는 현상을, 마치 입자가 외부의 열 에너지(KBT)를 흡수해서 장벽(ΔU)을 넘어가는 과정으로 설명합니다. 이 전이율(탈출 빈도)은 볼츠만 인자(Boltzmann Factor)에 따라 지수 함수적으로 온도에 의존하게 돼요. 즉, 온도가 낮아질수록 전이율은 급격하게, 거의 0에 가깝게 줄어듭니다. 고전적인 관점에서는 이게 당연한 이야기잖아요. 충분히 낮은 온도에서는 에너지를 공급받기 어려우니 우물을 벗어날 수 없다는 거죠.
반면에, 양자 터널링(Quantum Tunneling) 이론은 온도의 영향을 받지 않습니다. 양자 역학에 따르면, 입자는 장벽을 넘는 것이 아니라 장벽을 '투과'합니다. 이 터널링 확률 (𝛤₍𝓺𝓾𝓪𝓷𝓽𝓾𝓶₎) 은 오직 시스템의 양자 역학적 특성(퍼텐셜 장벽의 모양, 유효 질량 등)에만 의존하며, 절대 0도에서도 유한한 값을 가집니다.
Devoret 팀은 바로 이 결정적인 차이를 공략했어요. 그들은 접합의 탈출 빈도를 다양한 온도에서 측정했습니다. 측정 결과를 온도에 대한 그래프로 그려보니, 높은 온도(100 mK 이상)에서는 데이터가 고전적 활성화 이론의 예측 (𝛤ₜₕₑᵣₘₐₗ)을 매우 잘 따랐습니다. 하지만 온도가 점점 낮아져 교차 온도 Tcrossover 이하로 떨어지자, 탈출 빈도는 더 이상 온도에 따라 급격히 감소하지 않고, 평평하게 수평을 유지하는 현상이 관측되었습니다.
이 잔류 탈출 빈도 값은 고전적 이론으로는 도저히 설명할 수 없는 것이었어요. 그리고 중요한 것은, 이 값이 WKB 근사를 이용한 양자 터널링 이론의 예측치와 거의 완벽하게 일치했다는 점입니다. 이 명쾌한 실험적 증거는 더 이상 이 현상을 고전적인 열 잡음으로 치부할 수 없게 만들었고, 거시적 양자 터널링 현상의 실재를 물리학계에 각인시키는 결정적인 순간이 되었습니다.
| 구분 | 이론 | 주요 특징 (탈출 빈도 𝛤) |
|---|---|---|
| 고전적 영역 | 열 활성화 (Thermal Activation) | 온도(T)에 지수 함수적으로 의존. T→0 이면 𝛤 는 0으로 급감. |
| 양자 영역 | 양자 터널링 (Quantum Tunneling) | 온도에 무관하며, T=0 에서도 유한한 잔류 값 가짐. 시스템 특성에만 의존. |
이 비교 분석은 물리학적 현상을 검증하는 교과서적인 방법을 보여줍니다. 두 상반된 이론의 예측치를 대비시키고, 실험으로 그 경계를 명확히 구분해 낸 거죠. 이 논문의 성공은 단순히 거시적 양자 터널링을 증명하는 것을 넘어, 초전도 회로 내의 양자 역학적 거동을 예측하고 제어할 수 있는 수학적 도구가 얼마나 정확한지를 보여줬다는 점에서 큰 의미가 있어요. 이러한 정량적인 검증이 없었다면, 후속 연구자들이 초전도 큐비트 개발에 확신을 가지기 어려웠을 겁니다. 이 논문이 과학적 논리의 정수를 보여준다고 생각하면, 정말 멋지지 않나요? 이로써 우리는 거시적인 스케일에서도 양자 역학이 우리의 우주를 지배하는 근본 원리임을 다시 한번 확인하게 됩니다. 이 놀라운 통찰력을 제공한 저자들에게 박수를 보내고 싶어요.
후속 연구와 현대 물리학에 미친 파급 효과
Devoret, Martinis, Clarke의 거시적 양자 터널링(MQT) 측정 논문은 단순한 '발표'를 넘어, 이후 수십 년간의 응집 물질 물리학(Condensed Matter Physics)과 양자 정보 과학(Quantum Information Science) 연구에 엄청난 파급 효과를 미쳤습니다. 이 논문이 없었다면 오늘날의 초전도 큐비트 기술은 상상하기 어려웠을 거예요. 마치 뉴턴의 만유인력 법칙이 고전 물리학의 시대를 열었듯이, 이 논문은 거시적 양자 제어의 시대를 열었다고 해도 과언이 아닙니다.
가장 직접적인 파급 효과는 당연히 초전도 큐비트 분야입니다. 이 논문은 조셉슨 접합이 양자 중첩 상태를 가질 수 있는 메타안정 퍼텐셜 우물을 형성한다는 이론적, 실험적 증거를 제공했어요. 이 아이디어를 바탕으로, J. Martinis를 포함한 저자들은 이후에 전하 큐비트(Charge Qubit), 플럭스 큐비트(Flux Qubit), 그리고 현재 가장 널리 사용되는 트랜스몬 큐비트(Transmon Qubit) 개발에 직접적으로 참여하거나 영감을 주었습니다. 특히, 거시적 양자 터널링의 정량적인 측정 성공은 큐비트의 설계 단계에서 결맞음 시간(Coherence Time)을 늘리는 데 필요한 환경 노이즈 제어 기술을 발전시키는 데 결정적인 역할을 했어요.
뿐만 아니라, 이 연구는 양자 측정(Quantum Measurement) 자체의 이해에도 큰 영향을 미쳤습니다. 거시적 양자 터널링 전이 과정을 측정하는 것은 곧, 양자 상태가 어떻게 붕괴(Collapse)하여 고전적인 상태(전압 상태)로 바뀌는지를 관찰하는 것과 같았거든요. 후속 연구자들은 이 시스템을 이용해 양자 비파괴 측정(Quantum Nondemolition Measurement, QND) 기법을 개발하고, 큐비트의 상태를 읽어내는(Readout) 정교한 기술을 발전시키는 데 이 논문의 통찰을 활용했습니다. 측정 자체가 양자 상태에 미치는 영향을 최소화하는 것이 양자 컴퓨팅에서는 매우 중요한데, 이 모든 과정의 시작점이 바로 거시적 양자 터널링을 이해하는 것이었어요.
후속 연구에 미친 영향 (H3)
- 초전도 큐비트의 탄생: 조셉슨 접합이 양자 시스템임을 확립하여 Charge, Flux, Transmon 큐비트 개발의 토대를 마련했어요.
- 양자 결맞음 연구 심화: 거시적 스케일에서의 결맞음 시간과 환경 잡음의 관계를 정량적으로 연구하는 시발점이 되었습니다.
- 양자 측정 기법 개발: MQT 탈출 메커니즘을 이해함으로써 큐비트의 상태 읽기(Readout) 및 QND 측정 기술이 비약적으로 발전했습니다.
이 논문의 또 다른 중요한 기여는 퀀텀 리미트(Quantum Limit)의 실제적인 도달 가능성을 보여줬다는 점입니다. 아무리 정교한 실험 장치라도 잡음이 있기 마련인데, 저자들은 극저온 냉각과 철저한 차폐를 통해 실험 장치를 열 잡음의 영향이 사라지는 '퀀텀 리미트'까지 끌어내렸어요. 이것은 단지 실험 기술의 발전이 아니라, 거시적 양자 시스템을 다루는 모든 연구 분야에 '어디까지 잡음을 줄여야 양자 효과를 볼 수 있는지'에 대한 실질적인 기준을 제시해 준 것이나 마찬가지입니다.
결론적으로, Devoret, Martinis, Clarke의 연구는 거시적 양자 터널링을 단순한 이론적 호기심의 대상이 아닌, 제어 가능하고 측정 가능한 물리적 현상으로 확립했습니다. 이 논문이 초전도 물리학과 양자 정보 분야에 미친 영향은 정말이지 대단해요. 이 논문이 없었다면, 아마도 우리는 여전히 '과연 거시적인 시스템에서 양자 역학이 가능할까?'라는 질문에 머물러 있었을지 모릅니다. 정말 흥미진진한 연구가 아닐 수 없습니다! 이 선구적인 발걸음 덕분에 우리가 지금 양자 컴퓨터의 미래를 논할 수 있다는 사실에 다시 한번 감사하게 되네요.
논문에서 제시된 정량적 데이터의 의미와 예측력
이 논문의 진정한 힘은 바로 정량적인 데이터와 이론적 예측의 완벽한 일치에서 나옵니다. 과학에서 '존재한다'를 주장하는 것보다 훨씬 어려운 것이 '얼마나, 어떻게' 존재하는지를 수치적으로 증명하는 거잖아요. Devoret, Martinis, Clarke는 거시적 양자 터널링의 존재를 입증했을 뿐만 아니라, 터널링 빈도( 𝛤 )의 크기와 편향 전류(I)에 대한 의존성을 이론과 거의 오차 없이 일치시켰어요. 이게 진짜 대단한 점이죠!
앞서 언급했듯이, MQT 이론은 탈출 빈도를 WKB 근사라는 양자 역학적 방법으로 계산합니다. 이 근사는 퍼텐셜 장벽을 통과할 확률을 계산하는 데 사용되는데, 이 확률은 장벽의 높이, 폭, 그리고 입자의 유효 질량에 매우 민감하게 의존하죠. 논문에서 저자들은 접합의 임계 전류(I0)와 커패시턴스(C) 값을 정밀하게 측정하고, 이를 이론적 모델에 대입하여 거시적 양자 터널링 빈도를 예측했습니다.
그들이 제시한 그래프들을 보면, 저온 영역에서 측정된 탈출 빈도 데이터 포인트가 이론적인 WKB 곡선 위에 거의 정확하게 놓여 있습니다. 특히 편향 전류(I)가 증가함에 따라 탈출 빈도가 지수 함수적으로 증가하는 패턴이 이론 예측과 완벽하게 일치하는 것을 보고 정말 전율을 느꼈어요. 이 일치는 단순히 현상을 관측한 것을 넘어, 양자 역학이 거시적인 스케일에서도 정확한 예측 도구임을 입증한 것입니다.
거시적 양자 터널링 연구에서 이론과 실험의 정량적 일치는 핵심이에요. 이는 조셉슨 접합을 기반으로 한 양자 큐비트 설계 시, 에너지 준위와 전이 확률을 정밀하게 예측할 수 있는 기반이 되었기 때문입니다. 믿을 수 있는 수치가 있어야 다음 단계로 나아갈 수 있잖아요!
이러한 정량적 예측력은 특히 교차 온도(TCROSSOVER)의 계산에서도 빛을 발했습니다. 이 논문은 열 활성화 영역(T > TCROSSOVER)과 거시적 양자 터널링 영역(T < TCROSSOVER) 사이의 경계가 시스템의 특성(I0와 C)에 의해 정확히 계산될 수 있음을 보여줬고,실제 실험에서 관측된 잔류 탈출 빈도가 발생하는 온도가 이 이론적 예측치와 매우 근접했어요.
또 하나 주목할 만한 점은, 이 정량적 데이터가 조셉슨 접합의 파라미터를 정확하게 측정하는 것의 중요성을 강조했다는 점이에요. 임계 전류(I0)와 커패시턴스(C) 값에 작은 오차가 있어도, 탈출 빈도의 예측치는 크게 달라질 수 있거든요. 저자들은 이 파라미터들을 독립적인 실험(예: 고전적 열 활성화 영역에서의 측정)을 통해 먼저 정밀하게 결정하고, 그 값을 거시적 양자 터널링 이론에 대입하여 예측치를 얻었습니다. 이러한 독립적인 파라미터 결정 과정은 실험의 신뢰성을 극대화하는 데 결정적인 역할을 했어요.
결과적으로, 이 논문의 정량적 성과는 거시적 양자 터널링이 단순한 현상이 아니라, 조셉슨 접합의 기본 양자 역학적 특성임을 강력하게 입증했습니다. 이 예측력 덕분에 초전도 회로를 이용한 양자역학 연구는 더욱 정밀하고 신뢰성 있는 방향으로 발전할 수 있었죠. 수많은 초전도 큐비트 논문들이 이 논문의 정량적 모델을 기반으로 큐비트의 에너지 준위를 설계하고 제어하고 있다는 사실을 생각해보면, 이 데이터가 현대 물리학에 미친 기여는 정말 헤아릴 수 없을 정도입니다. 이처럼 깔끔하고 설득력 있는 정량적 결과는 학습 노트 작성자인 저에게도 깊은 인상을 남겼습니다. 정말 잘 짜여진 과학적 보고서의 정석을 보는 느낌이었어요.
거시적 양자 터널링 측정의 기술적 난이도와 극복 과정
이 논문을 읽으면서 가장 감탄했던 부분 중 하나는 바로 실험의 기술적 난이도와 저자들이 그것을 어떻게 극복했는지에 대한 이야기였어요. 거시적 양자 터널링 측정은 이론만큼이나 실험적으로도 엄청난 도전을 요구합니다. 왜냐하면 MQT 현상은 극도로 낮은 온도와 완벽에 가까운 잡음 격리가 필요하기 때문이죠. 조금이라도 외부 에너지가 유입되면 양자 터널링 대신 고전적인 열 활성화 전이가 우세하게 나타나거든요.
첫 번째 기술적 난관은 당연히 극저온 환경이었습니다. 거시적 양자 터널링이 열 활성화보다 우세해지는 교차 온도(TCROSSOVER)가 수십 밀리켈빈(mK) 수준이었기 때문에, 저자들은 헬륨-3/헬륨-4 희석 냉장고(Dilution Refrigerator)를 사용하여 샘플을 이 온도로 냉각해야 했습니다. 이 희석 냉각 기술 자체가 당시에도 최첨단이었고, 이 낮은 온도에서 전기적인 측정 장치를 안정적으로 작동시키는 것이 또 하나의 큰 과제였어요. mK 단위의 온도에서 정밀한 측정을 하는 것은 정말 지옥 같은 작업입니다.
두 번째이자 가장 중요한 난관은 환경 잡음(Environmental Noise)의 제거였습니다. 거시적 양자 터널링을 방해하는 잡음은 크게 두 가지로 나눌 수 있어요. 하나는 전자기파 노이즈이고, 다른 하나는 접합 자체의 내부 잡음(예: 2-레벨 시스템 노이즈)입니다. 저자들은 이 외부 노이즈를 막기 위해 다단계의 금속 차폐(Shielding)와 저역 통과 필터(Low-Pass Filter)를 사용했습니다. 특히, 측정에 사용되는 케이블을 통해 들어오는 고주파 노이즈는 접합의 퍼텐셜 장벽을 흔들어서 터널링을 촉진시킬 수 있었기 때문에, 이 필터링 작업이 정말 중요했다고 논문에서 강조하고 있어요.
거시적 양자 터널링 측정의 성공은 외부 전자기파 노이즈를 극도로 낮은 수준으로 억제했기 때문에 가능했어요. 이 잡음이 MQT 전이를 열 활성화처럼 보이게 만드는 주범이었고, 저자들의 철저한 필터링 전략이 없었다면 MQT의 명확한 증거를 얻을 수 없었을 겁니다.
측정 기법 자체도 대단했어요. 그들은 '히스토그램 방식(Histogram Method)'을 사용해서 접합이 제로 전압 상태에서 벗어나는 시간을 정밀하게 측정했습니다. 접합에 일정 전류를 가하고, 전압 상태로 넘어가는 순간을 포착한 후, 이 과정을 수없이 반복하여 탈출 시간 분포의 히스토그램을 얻어냈죠. 이 히스토그램의 형태(대략 지수 함수적 감쇠)로부터 탈출 빈도 (𝛤) 를 추출해냈습니다. 이 과정 자체가 엄청난 데이터 통계적 처리와 측정 자동화 기술을 요구했어요.
이러한 기술적 난이도를 극복하고 이론적 예측과 완벽하게 일치하는 깨끗한 데이터를 얻어냈다는 사실 자체가 Devoret, Martinis, Clarke의 연구팀이 얼마나 숙련된 실험 물리학자들이었는지 보여줍니다. 특히, 양자 컴퓨터의 핵심 기술인 노이즈 스펙트럼 분석과 초고감도 측정은 이 거시적 양자 터널링 연구에서부터 시작되었다고 봐도 무방해요. 이분들의 선구적인 기술력 덕분에 우리는 오늘날 더욱 복잡한 양자 회로를 다룰 수 있게 된 것입니다. 이 논문은 단순한 과학적 발견을 넘어, 정교한 실험 물리학의 정수를 보여주는 작품이라고 저는 생각해요. 대단합니다, 정말!
거시적 양자 터널링 현상의 물리적 의미와 고전적 한계
이제 이 거시적 양자 터널링(MQT) 현상이 우리에게 던져주는 물리적 의미에 대해 깊이 생각해 볼 차례예요. 이 현상은 단순히 하나의 실험 결과가 아니라, 거시 세계와 미시 세계를 가르는 경계에 대한 근본적인 질문을 던졌습니다. Devoret, Martinis, Clarke의 연구가 성공하기 전까지는, 대부분의 물리학자들은 양자 역학이 원자 수준에서만 의미가 있고, 수많은 입자로 이루어진 '거시적인' 시스템에서는 환경과의 상호작용(Decoherence) 때문에 양자적 특성이 사라질 것이라고 추측했어요.
하지만 조셉슨 접합에서 거시적 양자 터널링이 관측되었다는 것은, 수많은 초전도 전자쌍(쿠퍼 쌍)의 집단적인 거동을 나타내는 변수(위상차 δ)가 양자 역학의 법칙을 따르고 있음을 의미합니다. 이 위상차는 단순히 하나의 입자가 아니라 수많은 입자들의 거시적 상태를 대표하는 변수이거든요. 이 거시적 변수가 파동 함수(Wave Function)를 가지고 터널링을 한다는 사실은, 양자 역학이 보편적인 자연의 법칙이며, 특수한 미시 세계에만 적용되는 것이 아님을 강력하게 시사합니다.
이 현상은 특히 고전 물리학의 한계를 명확히 보여줍니다. 고전 물리학에서는 입자가 퍼텐셜 장벽을 통과하는 유일한 방법은 열 에너지를 얻어 장벽을 넘는 것뿐입니다. 하지만 거시적 양자 터널링 영역에서는 온도가 아무리 낮아져도 전이가 계속 일어나죠. 이는 열 에너지의 도움 없이도 시스템이 하나의 거시적 상태에서 다른 상태로 전이할 수 있음을 의미하며, 이는 순전히 양자 역학적 원리인 불확정성 원리(Uncertainty Principle)의 결과입니다.
고전적 한계의 돌파
고전 물리학은 ℏ → 0의 극한으로 설명할 수 있지만, 거시적 양자 터널링은 유한한 플랑크 상수(ℏ)의 효과가 거시적 스케일에서도 사라지지 않음을 보여줍니다. 즉, 양자 효과가 거시적인 변수의 동역학을 지배할 수 있다는 놀라운 증거인 거죠.
이 현상의 관측은 '슈뢰딩거의 고양이'와 같은 사고 실험에서 제기되는 거시적 양자 중첩의 문제를 현실적인 실험 환경으로 끌어내렸다는 점에서도 철학적인 의미가 깊습니다. 비록 이 실험이 직접적으로 중첩 상태를 관측한 것은 아니지만, 거시적 변수의 양자 역학적 거동이 가능하다는 것을 보여주었기 때문입니다.
또한, 이 논문은 조셉슨 접합을 유효 해밀토니언(Effective Hamiltonian)으로 설명할 수 있는 기반을 마련했습니다. 이 해밀토니언은 접합의 위상차(δ)와 그 켤레 변수(켤레 운동량, P)를 양자 역학적 연산자처럼 다룰 수 있게 해줍니다. 이로써 우리는 조셉슨 접합을 단순한 전기 회로가 아닌, 일종의 양자 진동자(Quantum Oscillator)로 해석하고, 그 에너지 준위와 전이를 계산할 수 있게 되었어요.
결론적으로, Devoret, Martinis, Clarke의 거시적 양자 터널링 연구는 양자 역학의 보편성을 실험적으로 입증한 기념비적인 업적이며, 고전 물리학의 경계를 넘어설 수 있는 길을 열어주었습니다. 이 놀라운 현상의 측정은 물리학의 기초 이론에 대한 우리의 이해를 한 단계 끌어올렸으며, 양자 기술의 혁명이라는 거대한 물결의 가장 첫 물방울이었다고 생각합니다. 이 논문을 읽고 나니, 거시 세계와 미시 세계를 구분하는 것이 얼마나 인위적인 일이었는지 새삼 깨닫게 되네요. 이 연구의 물리적, 철학적 의미는 정말 어마어마하다고밖에 말할 수 없습니다.
글의 핵심 요약: MQT 측정의 5가지 결정적 성과
지금까지 Devoret, Martinis, Clarke의 거시적 양자 터널링(MQT) 논문에 대해 자세히 알아봤는데요, 이 모든 내용을 한눈에 정리해 봅시다! 이 논문이 왜 초전도와 양자 정보 과학의 역사를 바꿨는지, 그 5가지 결정적인 성과를 다시 한번 되짚어 보는 건 정말 중요해요.
- MQT의 실험적 증명: 극저온 환경에서 조셉슨 접합의 탈출 빈도가 온도에 무관한 잔류 값을 가짐을 명확히 관측함으로써, 거시적 양자 터널링의 실재를 과학적으로 입증했습니다.
- 정량적 예측의 성공: 측정된 탈출 빈도(𝛤)가 WKB 근사를 이용한 양자 역학적 이론 예측치와 거의 완벽하게 일치함을 보여주어, 초전도 회로의 양자 역학적 모델의 정확성을 확립했습니다.
- 양자 컴퓨팅의 기반 마련: 조셉슨 접합을 제어 가능한 거시적 양자 시스템으로 확립하여, 초전도 기반 양자 큐비트 개발의 이론적, 실험적 출발점이 되었습니다.
- 열 활성화와의 경계 제시: 실험 데이터를 통해 고전적 활성화 영역과 양자 터널링 영역 사이의 교차 온도(TCROSSOVER)를 명확히 구분하여, 거시적 양자 효과를 관측할 수 있는 실험 조건을 제시했습니다.
- 기술적 혁신: 극저온 냉각, 초정밀 잡음 제어, 히스토그램 기반 통계적 측정 등 까다로운 실험 기술의 정수를 보여주어 후속 양자 실험의 기술적 기준을 제시했습니다.
이 다섯 가지 성과는 Devoret, Martinis, Clarke의 논문이 단순한 하나의 실험 보고서가 아니라, 현대 양자 물리학의 방향을 결정지은 핵심 이정표였음을 분명히 보여줍니다. 거시적 양자 터널링이라는 현상 자체가 물리학의 오랜 난제를 해결한 열쇠였다는 거죠.
자주 묻는 질문 ❓

Devoret, Martinis, Clarke의 거시적 양자 터널링 논문을 통해 양자 물리학의 짜릿한 순간을 함께 엿볼 수 있어서 정말 즐거웠어요!